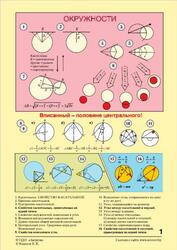
Предлагаемое вниманию читателя пособие содержит более 600 разноуровневых задач и упражнений по основным темам программы геометрии (планиметрии) 8 класса, скомпонованных в комплект по готовым чертежам, содержащий 24 таблицы.
Эти упражнения дают возможность учителю в течение минимума времени решить и повторить значительно больший объем материала и тем самым наращивать темп работы на уроках.
Кроме того, приводятся краткие теоретические сведения по курсу геометрии, сопровождаемые определениями, теоремами, основными свойствами и необходимыми справочными материалами. К наиболее трудным задачам приведены решения и указания. Задачи повышенной сложности отмечены знаком.
Пособие адресовано учителям математики, репетиторам, студентам — будущим учителям, учащимся общеобразовательных школ, лицеев, колледжей, а также выпускникам для подготовки к ОГЭ и ЕГЭ.