Уравнение с одной переменной.
Уравнение – это равенство, в котором присутствует одна или несколько переменных.
Мы рассмотрим случай, когда в уравнении одна переменная, то есть одно неизвестное число. По сути, уравнение – это вид математической модели. Поэтому в первую очередь уравнения необходимы нам для решения задач.
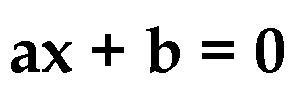
Вспомним, как составляется математическая модель для решения задачи.
Например, в новом учебном году количество учащихся в школе №5 увеличилось вдвое. После того, как 20 учеников перешли в другую школу, в общей сложности в школе №5 стало учиться 720 учеников. Сколько учащихся было в прошлом году?
Нам нужно выразить то, что сказано в условии математическим языком. Пусть количество учащихся в прошлом году будет X. Тогда согласно условию задачи,
2X – 20 = 720. У нас получилась математическая модель, которая представляет собой уравнение с одной переменной. Если точнее, то это уравнение первой степени с одной переменной. Осталось найти его корень.
Что такое корень уравнения?
То значение переменной, при котором наше уравнение обратится в верное равенство, называется корнем уравнения. Бывают такие уравнения, у которых много корней. Например, в уравнении 2*X = (5-3)*X любое значение X является корнем. А уравнение X = X +5 вообще не имеет корней, так как какое бы мы не подставили значение X, у нас не получится верное равенство. Решить уравнение означает найти все его корни, или определить, что оно не имеет корней. Таким образом, чтобы ответить на наш вопрос, нам нужно решить уравнение 2X – 20 = 720.
Как решать уравнения с одной переменной?
Для начала запишем базовые определения. Каждое уравнение имеет правую и левую части. В нашем случае, (2X – 20) – левая часть уравнения (она стоит слева от знака равенства), а 720 – правая часть уравнения. Слагаемые правой и левой части уравнения называются членами уравнения. У нас членами уравнения являются 2X, -20 и 720.
Сразу скажем про 2 свойства уравнений:
- Любой член уравнения можно переносить из правой части уравнения в левую, и наоборот. При этом надо изменить знак этого члена уравнения на противоположный. То есть, записи вида 2X – 20 = 720, 2X – 20 – 720 = 0, 2X = 720 + 20, -20 = 720 – 2X равносильны.
- Обе части уравнения можно умножить или разделить на одно и то же число. Это число не должно быть равно нулю. То есть, записи вида 2X – 20 = 720, 5*(2X – 20) = 720*5, (2X – 20):2 = 720:2 также равносильны.
Воспользуемся этими свойствами для решения нашего уравнения.
2X – 20 = 720
Перенесем -20 в правую часть с противоположным знаком. Получим:
2X = 720 + 20. Сложим то, что у нас в правой части. Получим, что 2X = 740.
Теперь разделим левую и правую части уравнения на 2.
2X:2 = 740:2 или X = 370. Мы нашли корень нашего уравнения и заодно нашли ответ на вопрос нашей задачи. В прошлом году в школе №5 было 370 учеников.
Проверим, действительно ли наш корень обращает уравнение в верное равенство. Подставим вместо X число 370 в уравнение 2X – 20 = 720.
2*370-20 = 720.
740-20 = 720
720 = 720.
Все верно.
Итак, чтобы решить уравнение с одной переменной его нужно привести к так называемому линейному уравнению вида ax = b, где a и b – некоторые числа. Затем левую и правую часть разделить на число a. Получим, что x = b:a.
Что означает привести уравнение к линейному уравнению?
Рассмотрим такое уравнение:
5X - 2X + 10 = 59 - 7X +3X.
Это также уравнение с одной неизвестной переменной X. Наша задача привести это уравнение к виду ax = b.
Для этого сначала соберем все слагаемые, имеющие в качестве множителя X в левой части уравнения, а остальные слагаемые - в правой части. Слагаемые, имеющие в качестве множителя одну и ту же букву, называют подобными слагаемыми.
5X - 2X + 7X – 3X = 59 – 10.
Согласно распределительному свойству умножения мы можем вынести одинаковый множитель за скобки, а коэффициенты (множители при переменной x) сложить. Этот процесс также называют приведением подобных слагаемых.
X(5-2+7-3) = 49.
7X = 49. Мы привели уравнение к виду ax = b, где a = 7, b = 49.
А как мы написали выше, корнем уравнения вида ax = b будет x = b:a.
То есть X = 49:7 = 7.
Алгоритм нахождения корней уравнения с одной переменной.
- Собрать подобные слагаемые в левой части уравнения, остальные слагаемые – в правой части уравнения.
- Привести подобные слагаемые.
- Привести уравнение к виду ax = b.
- Найти корни по формуле x = b:a.
Примечание. В данной статье мы не рассматривали те случаи, когда переменная возводится в какую-нибдуь степень. Иначе говоря мы рассматривали уравнения первой степени с одной переменной.
Дата публикации:
Теги: алгебра :: 7 класс :: уравнения
Смотрите также учебники, книги и учебные материалы:
Следующие учебники и книги:
Предыдущие статьи: